«1. Введение
Java предоставляет некоторые примитивы, такие как int или long, для выполнения целочисленных операций. Но иногда нам нужно хранить числа, которые превышают доступные ограничения для этих типов данных.
В этом уроке мы более подробно рассмотрим класс BigInteger. Мы проверим его структуру, заглянув в исходный код, и ответим на вопрос — как можно хранить большие числа за пределами доступных примитивных типов данных?
2. Класс BigInteger
Как мы знаем, класс BigInteger используется для математических операций, которые включают вычисления очень больших целых чисел, больших, чем примитивный тип long. Он представляет неизменяемые целые числа произвольной точности.
Прежде чем идти дальше, давайте вспомним, что в Java все байты представлены в системе с дополнением до двух с использованием записи с прямым порядком байтов. Он хранит старший байт слова по наименьшему адресу памяти (наименьший индекс). Более того, первый бит байта также является битом знака. Давайте рассмотрим примеры значений байтов:
-
1000 0000 представляет -128 0111 1111 представляет 127 1111 1111 представляет -1
Итак, теперь давайте проверим исходный код и объясним, как он хранит заданные числа, превышающие доступные ограничения примитивов.
2.1. int signum
Свойство signum определяет знак BigInteger. Три целых числа представляют знак значения: -1 для отрицательных чисел, 0 для нуля, 1 для положительных чисел:
assertEquals(1, BigInteger.TEN.signum());
assertEquals(-1, BigInteger.TEN.negate().signum());
assertEquals(0, BigInteger.ZERO.signum());Помните, что BigInteger.ZERO должен иметь знак 0 из-за массива величин. Это значение гарантирует, что для каждого значения BigInteger существует ровно одно представление.
2.2. int[] mag
Вся магия класса BigInteger начинается со свойства mag. Он хранит заданное значение в массиве, используя двоичное представление, что позволяет опустить ограничения примитивных типов данных.
Кроме того, BigInteger группирует их в 32-битные порции — набор из четырех байтов. Из-за этого величина внутри определения класса объявлена как массив int:
int[] mag;
Этот массив содержит величину заданного значения в записи с обратным порядком байтов. Нулевой элемент этого массива является самым значительным целым числом величины. Давайте проверим это с помощью BigInteger(byte[] bytes):
assertEquals(new BigInteger("1"), new BigInteger(new byte[]{0b1}))
assertEquals(new BigInteger("2"), new BigInteger(new byte[]{0b10}))
assertEquals(new BigInteger("4"), new BigInteger(new byte[]{0b100}))Этот конструктор переводит заданный массив байтов, содержащий двоичное представление с дополнением до двух, в значение.
Так как существует переменная величины знака (signum), мы не используем первый бит в качестве знакового бита значения. Давайте быстро проверим это:
byte[] bytes = { -128 }; // 1000 0000
assertEquals(new BigInteger("128"), new BigInteger(1, bytes));
assertEquals(new BigInteger("-128"), new BigInteger(-1, bytes));Мы создали два разных значения, используя конструктор BigInteger(int signum, byte[] величина). Он переводит представление величины знака в BigInteger. Мы повторно использовали тот же массив байтов, изменив только значение знака.
Мы также можем напечатать величину, используя метод toString(int radix):
assertEquals("10000000", new BigInteger(1, bytes));
assertEquals("-10000000", new BigInteger(-1, bytes));Обратите внимание, что для отрицательных значений добавляется знак минус.
Наконец, самое значимое значение int должно быть ненулевым. Это означает, что BigInteger.ZERO имеет массив mag нулевой длины:
assertEquals(0, BigInteger.ZERO.bitCount());
assertEquals(BigInteger.ZERO, new BigInteger(0, new byte[]{}));Сейчас мы пропустим проверку других свойств. Они помечены как устаревшие из-за избыточности и используются только как внутренний кеш.
Давайте теперь перейдем к более сложным примерам и проверим, как BigInteger хранит числа в примитивных типах данных.
3. BigInteger больше, чем Long.MAX_VALUE.
Как мы уже знаем, тип данных long представляет собой 64-битное целое число с дополнением до двух. Signed long имеет минимальное значение -263 (1000 0000 … 0000) и максимальное значение 263-1 (0111 1111 … 1111). Чтобы создать число, превышающее эти пределы, нам нужно использовать класс BigInteger.
Давайте теперь создадим значение на единицу больше, чем Long.MAX_VALUE, равное 263. Согласно информации из предыдущей главы, оно должно иметь:
-
свойство signum, установленное в 1, массив mag, с 64 общее количество битов, где установлен только старший бит (1000 0000 … 0000).
Во-первых, давайте создадим BigInteger с помощью функции setBit(int n):
BigInteger bi1 = BigInteger.ZERO.setBit(63);
String str = bi1.toString(2);
assertEquals(64, bi1.bitLength());
assertEquals(1, bi1.signum());
assertEquals("9223372036854775808", bi1.toString());
assertEquals(BigInteger.ONE, bi1.substract(BigInteger.valueOf(Long.MAX_VALUE)));
assertEquals(64, str.length());
assertTrue(str.matches("^10{63}$")); // 1000 0000 ... 0000«
«Помните, что в двоичной системе представления биты упорядочены справа налево, начиная с 0. В то время как BigInteger.ZERO имеет пустой массив величин, установка 63-го бита делает его одновременно и самым значащим — нулевым элементом. из массива 64 длины. Знак автоматически устанавливается равным единице.
byte[] bytes = ByteBuffer.allocate(Long.BYTES).putLong(Long.MIN_VALUE).array();
BigInteger bi2 = new BigInteger(1, bytes);
assertEquals(bi1, bi2);
...С другой стороны, та же последовательность битов представлена Long.MIN_VALUE. Преобразуем эту константу в массив byte[] и создадим конструкцию BigInteger:
Как видим, оба значения равны, поэтому применяется один и тот же пакет утверждений.
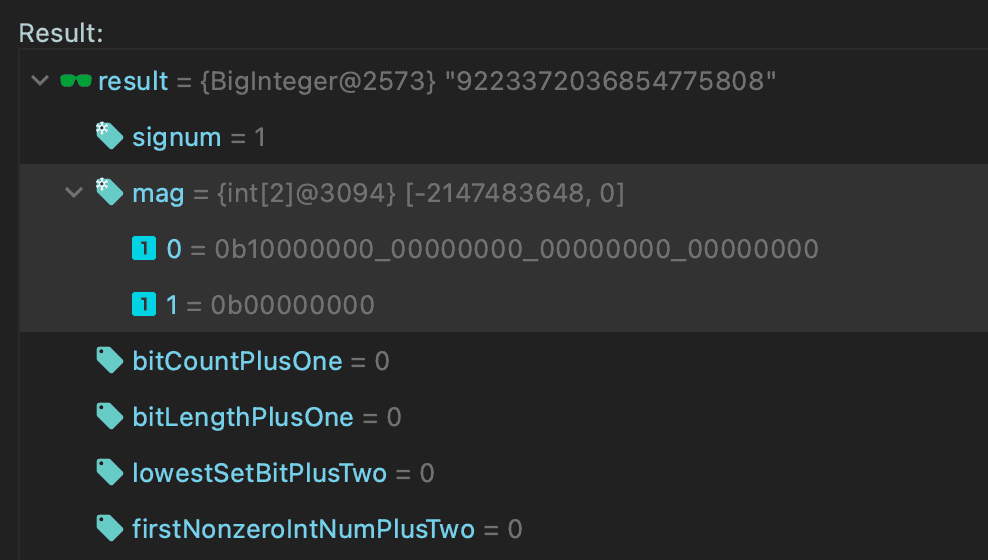
Наконец, мы можем проверить внутреннюю переменную int[] mag. В настоящее время Java не предоставляет API для получения этого значения, но мы можем сделать это с помощью инструмента оценки в нашем отладчике:
Мы сохраняем наше значение в массиве, используя два целых числа, два пакета по 32 бита. Нулевой элемент равен Integer.MIN_VALUE, а другой равен нулю.
4. Заключение
В этом кратком руководстве мы сосредоточились на деталях реализации класса BigInteger. Мы начали с того, что напомнили некоторую информацию о числах, примитивах и правилах двоичного представления.
Затем мы проверили исходный код BigInteger. Мы проверили свойства signum и mag. Мы также узнали, как BigInteger хранит данное значение, что позволяет нам предоставлять большие числа, чем доступные примитивные типы данных.