«1. Обзор
В этом кратком руководстве мы узнаем, как мы можем обнаружить цикл в заданном ориентированном графе.
2. Представление графа
В этом уроке мы будем придерживаться представления графа списка смежности.
Во-первых, давайте начнем с определения вершины в Java:
public class Vertex {
private String label;
private boolean beingVisited;
private boolean visited;
private List<Vertex> adjacencyList;
public Vertex(String label) {
this.label = label;
this.adjacencyList = new ArrayList<>();
}
public void addNeighbor(Vertex adjacent) {
this.adjacencyList.add(adjacent);
}
//getters and setters
}Здесь adjacencyList вершины v содержит список всех вершин, смежных с v. Метод addNeighbor() добавляет соседнюю вершину к соседству list of v.
Мы также определили два логических параметра, посещенных и посещенных, которые показывают, посещается ли узел в настоящее время или уже был посещен.
Граф можно рассматривать как группу вершин или узлов, соединенных ребрами.
Итак, давайте теперь быстро представим граф в Java:
public class Graph {
private List<Vertex> vertices;
public Graph() {
this.vertices = new ArrayList<>();
}
public void addVertex(Vertex vertex) {
this.vertices.add(vertex);
}
public void addEdge(Vertex from, Vertex to) {
from.addNeighbor(to);
}
// ...
}Мы будем использовать методы addVertex() и addEdge() для добавления новых вершин и ребер в наш граф.
3. Обнаружение циклов
Чтобы обнаружить цикл в ориентированном графе, мы будем использовать вариант обхода в глубину:
-
Выберите непосещенную вершину v и отметьте ее состояние как посещенное Для каждой соседней вершины u из v, проверьте: если u уже находится в состоянии BeingVisited, это явно означает, что существует обратная граница и, следовательно, обнаружен цикл. флаг вершины v’s bevisited установлен на false, а флаг ее посещения — на true
Обратите внимание, что все вершины нашего графа изначально находятся в состоянии unvisited, так как их флаги beingVisited и посещенные инициализированы значением false.
Давайте теперь посмотрим на наше Java-решение:
public boolean hasCycle(Vertex sourceVertex) {
sourceVertex.setBeingVisited(true);
for (Vertex neighbor : sourceVertex.getAdjacencyList()) {
if (neighbor.isBeingVisited()) {
// backward edge exists
return true;
} else if (!neighbor.isVisited() && hasCycle(neighbor)) {
return true;
}
}
sourceVertex.setBeingVisited(false);
sourceVertex.setVisited(true);
return false;
}Мы можем использовать любую вершину графа в качестве исходной или начальной вершины.
Для несвязанного графа нам придется добавить дополнительный метод-оболочку:
public boolean hasCycle() {
for (Vertex vertex : vertices) {
if (!vertex.isVisited() && hasCycle(vertex)) {
return true;
}
}
return false;
}Это гарантирует, что мы посещаем каждый компонент несвязанного графа для обнаружения цикла.
4. Тестирование реализации
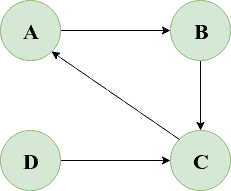
Давайте рассмотрим приведенный ниже циклический ориентированный граф:
Мы можем быстро написать JUnit для проверки нашего метода hasCycle() для этого графа:
@Test
public void givenGraph_whenCycleExists_thenReturnTrue() {
Vertex vertexA = new Vertex("A");
Vertex vertexB = new Vertex("B");
Vertex vertexC = new Vertex("C")
Vertex vertexD = new Vertex("D");
Graph graph = new Graph();
graph.addVertex(vertexA);
graph.addVertex(vertexB);
graph.addVertex(vertexC);
graph.addVertex(vertexD);
graph.addEdge(vertexA, vertexB);
graph.addEdge(vertexB, vertexC);
graph.addEdge(vertexC, vertexA);
graph.addEdge(vertexD, vertexC);
assertTrue(graph.hasCycle());
}Здесь наш hasCycle() метод вернул true, что означает, что наш график является циклическим.
5. Заключение
В этом уроке мы узнали, как проверить, существует ли цикл в заданном ориентированном графе в Java.
Как обычно, реализация кода с примерами доступна на Github.