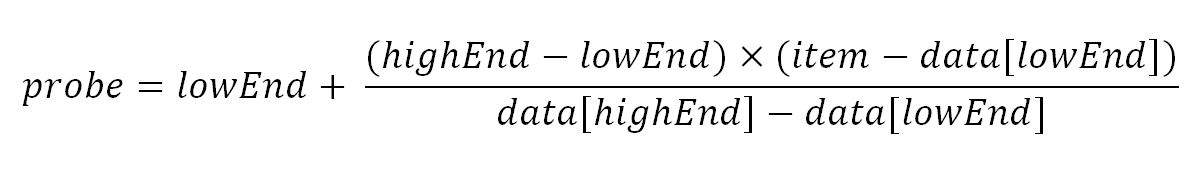«1. Введение
В этом уроке мы рассмотрим алгоритмы интерполяционного поиска и обсудим их плюсы и минусы. Кроме того, мы реализуем его на Java и поговорим о временной сложности алгоритма.
2. Мотивация
Интерполяционный поиск — это усовершенствование бинарного поиска, предназначенное для равномерно распределенных данных.
Бинарный поиск разделяет пространство поиска вдвое на каждом шаге независимо от распределения данных, поэтому временная сложность всегда равна O(log(n)).
С другой стороны, сложность времени интерполяционного поиска зависит от распределения данных. Это быстрее, чем бинарный поиск для равномерно распределенных данных с временной сложностью O(log(log(n))). Однако в худшем случае он может работать так же плохо, как O (n).
3. Поиск с интерполяцией
Подобно бинарному поиску, поиск с интерполяцией может работать только в отсортированном массиве. Он помещает зонд в рассчитанное положение на каждой итерации. Если щуп находится прямо на искомом элементе, позиция будет возвращена; в противном случае пространство поиска будет ограничено либо правой, либо левой стороной зонда.
Вычисление положения зонда — единственное различие между бинарным поиском и поиском с интерполяцией.
В бинарном поиске позиция зонда всегда является самым средним элементом оставшегося пространства поиска.
Наоборот, поиск с интерполяцией вычисляет положение зонда по следующей формуле:
Давайте рассмотрим каждый из терминов:
-
зонд: этому параметру будет присвоено новое положение зонда. lowEnd: индекс самого левого элемента в текущей области поиска. highEnd: индекс самого правого элемента в текущем пространстве поиска. data[]: массив, содержащий исходное пространство поиска. item: предмет, который мы ищем.
Чтобы лучше понять, как работает интерполяционный поиск, давайте продемонстрируем его на примере.
Допустим, мы хотим найти позицию 84 в массиве ниже:
Длина массива равна 8, поэтому изначально highEnd = 7 и lowEnd = 0 (поскольку индекс массива начинается с 0, а не с 1).
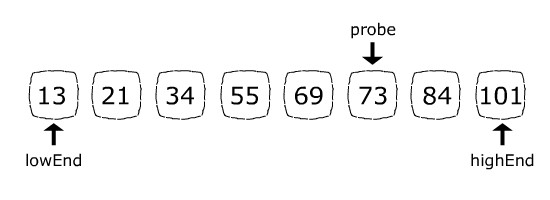
На первом шаге формула положения зонда даст зонд = 5:
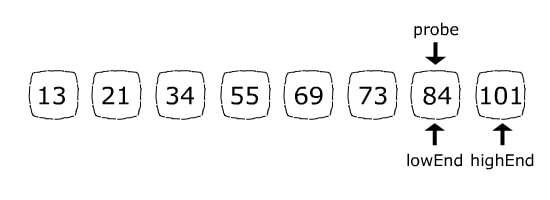
Поскольку 84 (элемент, который мы ищем) больше, чем 73 (текущий элемент положения зонда), на следующем шаге мы откажемся от левой части массива, назначив lowEnd = probe + 1. Теперь пространство поиска состоит только из 84 и 101. Формула положения датчика установит probe = 6, что точно соответствует индексу 84:
Так как элемент, который мы искали, найдена, будет возвращена позиция 6.
4. Реализация на Java
Теперь, когда мы поняли, как работает алгоритм, давайте реализуем его на Java.
Сначала мы инициализируем lowEnd и highEnd:
int highEnd = (data.length - 1);
int lowEnd = 0;Затем мы настраиваем цикл и на каждой итерации вычисляем новый зонд на основе вышеупомянутой формулы. Условие цикла гарантирует, что мы не вышли за пределы области поиска, сравнивая элемент с данными [lowEnd] и данными [highEnd]:
while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {
int probe
= lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);
}Мы также проверяем, нашли ли мы элемент после каждого нового назначения зонда.
Наконец, мы настраиваем lowEnd или highEnd для уменьшения пространства поиска на каждой итерации:
public int interpolationSearch(int[] data, int item) {
int highEnd = (data.length - 1);
int lowEnd = 0;
while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {
int probe
= lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);
if (highEnd == lowEnd) {
if (data[lowEnd] == item) {
return lowEnd;
} else {
return -1;
}
}
if (data[probe] == item) {
return probe;
}
if (data[probe] < item) {
lowEnd = probe + 1;
} else {
highEnd = probe - 1;
}
}
return -1;
}5. Заключение
В этой статье мы рассмотрели интерполяционный поиск на примере. Мы также реализовали это на Java.
Примеры, показанные в этом руководстве, доступны на Github.