«1. Обзор
В этом уроке мы узнаем, как вычислить медиану потока целых чисел.
Мы продолжим постановку проблемы с примерами, затем проанализируем проблему и, наконец, реализуем несколько решений на Java.
2. Постановка задачи
Медиана — это среднее значение упорядоченного набора данных. Для набора целых чисел существует столько же элементов меньше медианы, сколько больше.
В упорядоченном наборе:
-
нечетного числа целых чисел средний элемент является медианой — в упорядоченном наборе { 5, 7, 10 } медиана составляет 7 четных чисел, середины нет элемент; медиана вычисляется как среднее двух средних элементов — в упорядоченном наборе {5, 7, 8, 10} медиана равна (7 + 8) / 2 = 7,5
Теперь давайте предположим, что вместо этого конечного множества, мы считываем целые числа из потока данных. Мы можем определить медиану потока целых чисел как медиану набора целых чисел, прочитанных до сих пор.
Формализуем постановку задачи. Получив входной поток целых чисел, мы должны разработать класс, который выполняет следующие две задачи для каждого прочитанного нами целого числа:
- Add the integer to the set of integers
- Find the median of the integers read so far
Например:
add 5 // sorted-set = { 5 }, size = 1
get median -> 5
add 7 // sorted-set = { 5, 7 }, size = 2
get median -> (5 + 7) / 2 = 6
add 10 // sorted-set = { 5, 7, 10 }, size = 3
get median -> 7
add 8 // sorted-set = { 5, 7, 8, 10 }, size = 4
get median -> (7 + 8) / 2 = 7.5
..
Хотя поток не является конечным, мы можем предположить что мы можем хранить все элементы потока в памяти одновременно.
Мы можем представить наши задачи в виде следующих операций в коде:
void add(int num);
double getMedian();
3. Наивный подход
3.1. Отсортированный список
Давайте начнем с простой идеи — мы можем вычислить медиану отсортированного списка целых чисел, обратившись к среднему элементу или двум средним элементам списка по индексу. Временная сложность операции getMedian составляет O(1).
Добавляя новое целое число, мы должны определить его правильную позицию в списке, чтобы список оставался отсортированным. Эта операция может быть выполнена за время O(n), где n — размер списка. Таким образом, общая стоимость добавления нового элемента в список и вычисления новой медианы составляет O(n).
3.2. Улучшение наивного подхода
Операция добавления выполняется за линейное время, что не является оптимальным. Попробуем рассмотреть это в этом разделе.
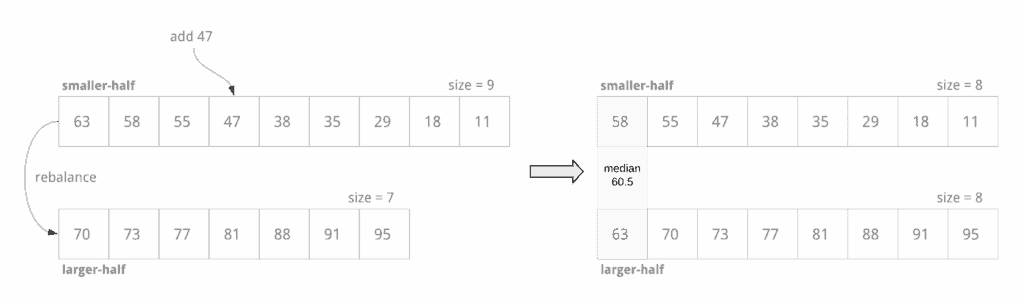
Мы можем разделить список на два отсортированных списка — меньшая половина целых чисел отсортирована в порядке убывания, а большая половина целых чисел — в порядке возрастания. Мы можем добавить новое целое число в соответствующую половину так, чтобы размер списков отличался не более чем на 1:
if element is smaller than min. element of larger half:
insert into smaller half at appropriate index
if smaller half is much bigger than larger half:
remove max. element of smaller half and insert at the beginning of larger half (rebalance)
else
insert into larger half at appropriate index:
if larger half is much bigger than smaller half:
remove min. element of larger half and insert at the beginning of smaller half (rebalance)
Теперь мы можем вычислить медиану:
if lists contain equal number of elements:
median = (max. element of smaller half + min. element of larger half) / 2
else if smaller half contains more elements:
median = max. element of smaller half
else if larger half contains more elements:
median = min. element of larger halfХотя мы только улучшили время сложности операции добавления на некоторый постоянный коэффициент, мы добились прогресса.
Давайте проанализируем элементы, к которым мы обращаемся в двух отсортированных списках. Потенциально мы получаем доступ к каждому элементу, когда сдвигаем их во время операции (сортированного) добавления. Что еще более важно, мы получаем доступ к минимуму и максимуму (экстремумам) большей и меньшей половин соответственно во время операции добавления для перебалансировки и во время операции getMedian.
Мы видим, что экстремумы являются первыми элементами соответствующих им списков. Таким образом, мы должны оптимизировать доступ к элементу с индексом 0 для каждой половины, чтобы улучшить общее время выполнения операции добавления.
4. Подход на основе кучи
Давайте уточним наше понимание проблемы, применяя то, что мы узнали из нашего наивного подхода:
- We must get the minimum/maximum element of a dataset in O(1) time
- The elements don’t have to be kept in a sorted order as long as we can get the minimum/maximum element efficiently
- We need to find an approach for adding an element to our dataset that costs less than O(n) time
Далее мы рассмотрим структуру данных кучи, которая помогает нам достичь наши цели эффективно.
4.1. Структура данных кучи
Куча — это структура данных, которая обычно реализуется с помощью массива, но может рассматриваться как двоичное дерево.
Кучи ограничены свойством кучи:
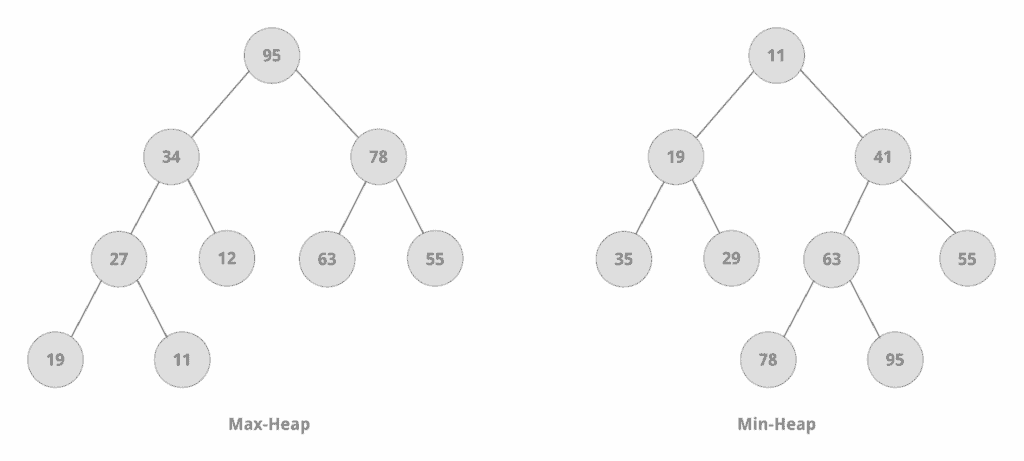
4.1.1. Max–heap Property
(дочерний) узел не может иметь значение больше, чем у его родителя. Следовательно, в максимальной куче корневой узел всегда имеет наибольшее значение.
4.1.2. Min–heap Property
Узел (родительский) не может иметь значение больше, чем у его дочерних элементов. Таким образом, в минимальной куче корневой узел всегда имеет наименьшее значение.
В Java класс PriorityQueue представляет кучу. Давайте перейдем к нашему первому решению с использованием кучи.
4.2. Первое решение
Давайте заменим списки в нашем наивном подходе двумя кучами:
-
«Минимальная куча, содержащая большую половину элементов, с минимальным элементом в корне Максимальная куча, содержащая меньшую половину элементов, с максимальным элементом в корне
Теперь мы можем добавить входящие целое число в соответствующую половину, сравнивая его с корнем минимальной кучи. Далее, если после вставки размер одной кучи отличается от размера другой кучи более чем на 1, мы можем перебалансировать кучи, тем самым сохраняя разницу в размерах не более 1:
if size(minHeap) > size(maxHeap) + 1:
remove root element of minHeap, insert into maxHeap
if size(maxHeap) > size(minHeap) + 1:
remove root element of maxHeap, insert into minHeapПри таком подходе мы может вычислить медиану как среднее значение корневых элементов обеих куч, если размер двух куч равен. В противном случае корневой элемент кучи с большим количеством элементов является медианой.
Мы будем использовать класс PriorityQueue для представления кучи. Свойство кучи PriorityQueue по умолчанию — min-heap. Мы можем создать max-heap, используя Comparator.reverserOrder, который использует порядок, обратный естественному:
class MedianOfIntegerStream {
private Queue<Integer> minHeap, maxHeap;
MedianOfIntegerStream() {
minHeap = new PriorityQueue<>();
maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
}
void add(int num) {
if (!minHeap.isEmpty() && num < minHeap.peek()) {
maxHeap.offer(num);
if (maxHeap.size() > minHeap.size() + 1) {
minHeap.offer(maxHeap.poll());
}
} else {
minHeap.offer(num);
if (minHeap.size() > maxHeap.size() + 1) {
maxHeap.offer(minHeap.poll());
}
}
}
double getMedian() {
int median;
if (minHeap.size() < maxHeap.size()) {
median = maxHeap.peek();
} else if (minHeap.size() > maxHeap.size()) {
median = minHeap.peek();
} else {
median = (minHeap.peek() + maxHeap.peek()) / 2;
}
return median;
}
}Прежде чем мы проанализируем время выполнения нашего кода, давайте посмотрим на временную сложность операций с кучей, которые у нас есть. used:
find-min/find-max O(1)
delete-min/delete-max O(log n)
insert O(log n)
Таким образом, операция getMedian может быть выполнена за время O(1), так как для нее требуются только функции find-min и find-max. Временная сложность операции добавления составляет O(log n) — три вызова вставки/удаления, каждый из которых требует O(log n) времени.
4.3. Решение, не зависящее от размера кучи
В нашем предыдущем подходе мы сравнивали каждый новый элемент с корневыми элементами кучи. Давайте рассмотрим другой подход с использованием кучи, в котором мы можем использовать свойство кучи для добавления нового элемента в соответствующую половину.
Как и в предыдущем решении, мы начинаем с двух куч — минимальной кучи и максимальной кучи. Далее введем условие: размер max-heap всегда должен быть (n/2), а размер min-heap может быть либо (n/2), либо (n/2) + 1, в зависимости от общего количества элементов в двух кучах. Другими словами, мы можем позволить только минимальной куче иметь дополнительный элемент, когда общее количество элементов нечетно.
С нашим постоянным размером кучи мы можем вычислить медиану как среднее значение корневых элементов обеих куч, если размеры обеих куч равны (n / 2). В противном случае корневым элементом минимальной кучи является медиана.
Когда мы добавляем новое целое число, у нас есть два сценария:
1. Total no. of existing elements is even
size(min-heap) == size(max-heap) == (n / 2)
2. Total no. of existing elements is odd
size(max-heap) == (n / 2)
size(min-heap) == (n / 2) + 1
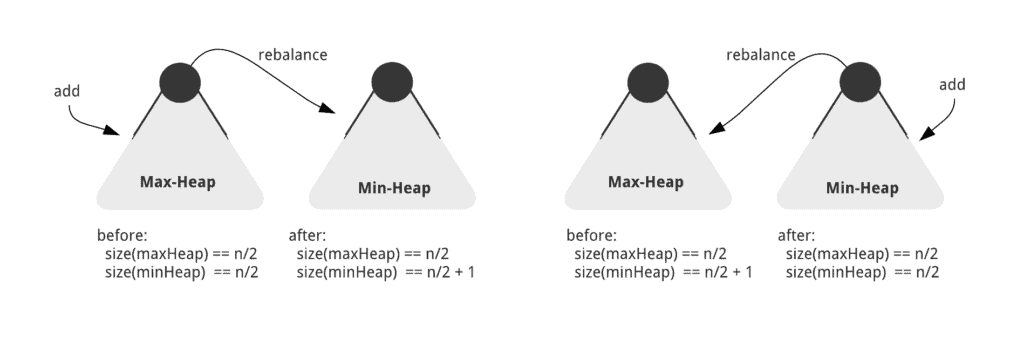
Мы можем поддерживать инвариант, добавляя новый элемент в одну из куч и каждый раз перебалансируя:
Перебалансировка работает путем перемещения самый большой элемент из максимальной кучи в минимальную кучу или путем перемещения наименьшего элемента из минимальной кучи в максимальную кучу. Таким образом, хотя мы не сравниваем новое целое число перед добавлением его в кучу, последующая перебалансировка гарантирует, что мы соблюдаем лежащий в основе инвариант меньших и больших половин.
Давайте реализуем наше решение на Java, используя PriorityQueues:
class MedianOfIntegerStream {
private Queue<Integer> minHeap, maxHeap;
MedianOfIntegerStream() {
minHeap = new PriorityQueue<>();
maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
}
void add(int num) {
if (minHeap.size() == maxHeap.size()) {
maxHeap.offer(num);
minHeap.offer(maxHeap.poll());
} else {
minHeap.offer(num);
maxHeap.offer(minHeap.poll());
}
}
double getMedian() {
int median;
if (minHeap.size() > maxHeap.size()) {
median = minHeap.peek();
} else {
median = (minHeap.peek() + maxHeap.peek()) / 2;
}
return median;
}
}Временные сложности наших операций остаются неизменными: getMedian стоит O(1) времени, а add выполняется за время O(log n) с точно таким же номером операций.
Оба решения на основе кучи предлагают схожие сложности с пространством и временем. Хотя второе решение умно и имеет более чистую реализацию, этот подход не интуитивно понятен. С другой стороны, первое решение естественно следует нашей интуиции, и легче рассуждать о правильности его операции сложения.
5. Заключение
В этом уроке мы научились вычислять медиану потока целых чисел. Мы оценили несколько подходов и реализовали несколько различных решений на Java с помощью PriorityQueue.
Как обычно, исходный код всех примеров доступен на GitHub.