«1. Обзор
Деревья — одна из самых важных структур данных в информатике. Обычно нас интересует сбалансированное дерево из-за его ценных свойств. Их структура позволяет выполнять такие операции, как запросы, вставки, удаления за логарифмическое время.
В этом уроке мы узнаем, как определить, сбалансировано ли бинарное дерево.
2. Определения
Во-первых, давайте введем несколько определений, чтобы убедиться, что мы находимся на одной странице: или два потомка Высота дерева – максимальное расстояние от корня до листа (такое же, как глубина самого глубокого листа) Сбалансированное дерево – вид дерева, в котором для каждого поддерева максимальное расстояние от от корня до любого листа не более чем на единицу больше, чем минимальное расстояние от корня до любого листа
-
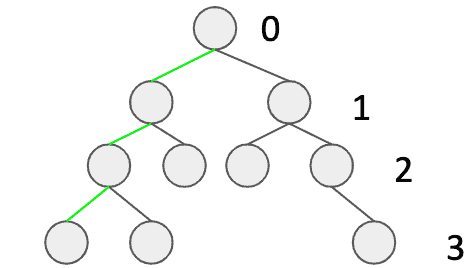
Мы можем найти пример сбалансированного бинарного дерева ниже. Три зеленых ребра — это простая визуализация того, как определить высоту, а цифры обозначают уровень.
3. Объекты предметной области
Итак, давайте начнем с класса для нашего дерева:
Для простоты предположим, что каждый узел имеет целочисленное значение. Обратите внимание, что если левое и правое деревья равны нулю, это означает, что наш узел является листом.
public class Tree {
private int value;
private Tree left;
private Tree right;
public Tree(int value, Tree left, Tree right) {
this.value = value;
this.left = left;
this.right = right;
}
}
Прежде чем представить наш основной метод, давайте посмотрим, что он должен возвращать:
Таким образом, для каждого отдельного вызова у нас будет информация о высоте и балансе.
private class Result {
private boolean isBalanced;
private int height;
private Result(boolean isBalanced, int height) {
this.isBalanced = isBalanced;
this.height = height;
}
}4. Алгоритм
Имея определение сбалансированного дерева, мы можем придумать алгоритм. Что нам нужно сделать, так это проверить желаемое свойство для каждого узла. Это может быть легко достигнуто с помощью рекурсивного обхода поиска в глубину.
Теперь наш рекурсивный метод будет вызываться для каждого узла. Кроме того, он будет отслеживать текущую глубину. Каждый вызов будет возвращать информацию о высоте и балансе.
Теперь давайте посмотрим на наш метод поиска в глубину:
Во-первых, нам нужно рассмотреть случай, когда наш узел равен нулю: мы вернем true (что означает, что дерево сбалансировано) и -1 как высота.
private Result isBalancedRecursive(Tree tree, int depth) {
if (tree == null) {
return new Result(true, -1);
}
Result leftSubtreeResult = isBalancedRecursive(tree.left(), depth + 1);
Result rightSubtreeResult = isBalancedRecursive(tree.right(), depth + 1);
boolean isBalanced = Math.abs(leftSubtreeResult.height - rightSubtreeResult.height) <= 1;
boolean subtreesAreBalanced = leftSubtreeResult.isBalanced && rightSubtreeResult.isBalanced;
int height = Math.max(leftSubtreeResult.height, rightSubtreeResult.height) + 1;
return new Result(isBalanced && subtreesAreBalanced, height);
}Затем мы делаем два рекурсивных вызова для левого и правого поддеревьев, сохраняя актуальность глубины.
На данный момент у нас есть вычисления, выполненные для дочерних элементов текущего узла. Теперь у нас есть все необходимые данные для проверки баланса:
переменная isBalanced проверяет высоту дочерних элементов, а substreesAreBalanced также указывает, сбалансированы ли оба поддеревья
-
Наконец, мы можем вернуть информацию о балансе и высоте. Также было бы неплохо упростить первый рекурсивный вызов методом фасада:
5. Резюме
public boolean isBalanced(Tree tree) {
return isBalancedRecursive(tree, -1).isBalanced;
}В этой статье мы обсудили, как определить, сбалансировано ли бинарное дерево. Мы объяснили подход поиска в глубину.
Как обычно, исходный код с тестами доступен на GitHub.
«